What Are Elliptic Curves?

Elliptic Curves Are Not Ellipses

Elliptic curves are not ellipses. An ellipse is a closed curve. A circle is a special case of an ellipse. Ellipses are pretty simple.

An elliptic curve, on the other hand, is a more complex smoothly curving shape. Potentially much more complex.

You can do operations of addition, negation, and multiplication on points on an elliptic curve. Those operations have exactly the same properties as they do with integers. But they work very differently.

Calculating powers, or chained multiplications, is easy and fast. But reversing that, calculating a discrete logarithm, is impractically difficult. There's your trapdoor.

The big two things to see here are the graphical illustration of addition on an elliptic curve, and how to calculate a set of points on a curve.

Let's see how those work.

Just A Little Math

I'm using MathJax to do math within HTML.

For me the first big epiphany was seeing the graphical version of addition on an elliptic curve and how much it differed from what I had naïvely expected. The second was figuring out how to do the modulo arithmetic to generate a set of curve points.

But before those big steps, we need to look at the elliptic curve. It is defined as the set of points (x,y) satisfying something called a Weierstrass equation: $$ y^2 + axy + by = x^3 + cx^2 + dx + e $$

However, we're looking to do cryptography, not to explore abstract mathematics.

The elliptic curves used in cryptography are simplified by setting some of the constants to zero or one: $$ y^2 + xy = x^3 + ax^2 + b $$

or even simpler, the frequently used: $$ y^2 = x^3 + ax + b $$

We are free to choose the constants, \(a\) and \(b\) in the two simplified equations above, so long as the discriminant \( \Delta \) is not zero: $$ \Delta = -16(4a^3 + 27b^2) \neq 0 $$

Below are some example curves for various integer values of \(a\) and \(b\). Notice the shape where they're both zero, when the determinant would also be zero. It has a cusp, where the curve goes into a corner and reverses direction. Other combinations of \(a\) and \(b\) yielding a determinant of zero generate a curve that crosses over themself. To be a real elliptic curve, the discriminant must be non-zero. No cusps, no crossings. A curve might be in one or two parts, if its discriminant is negative or positive, respectively. We see two-part curves here for \( a = 2 \) and \( b = \{-1, 0, 1\} \), and for \( a = 1 \) and \( b = 0 \).

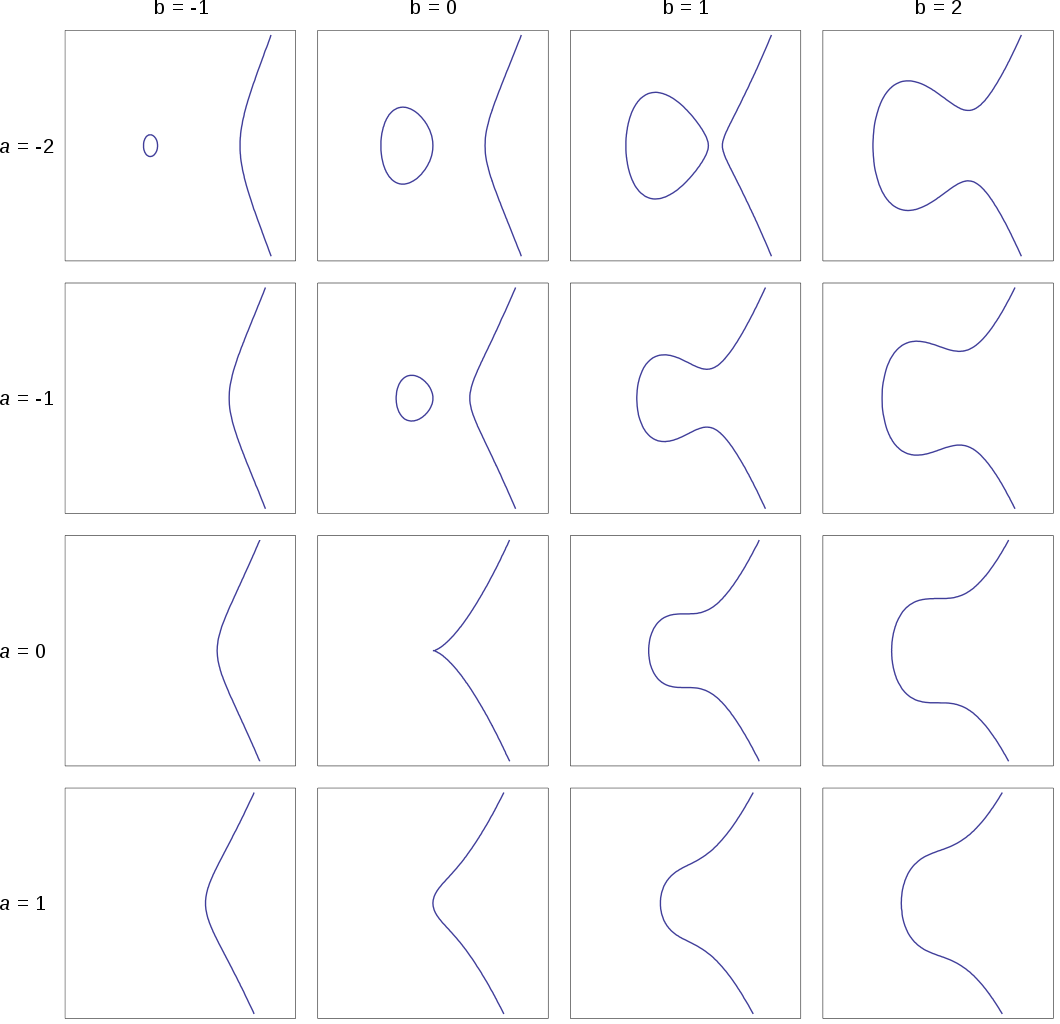
The constants \( a \) and \( b \) could be non-integer real numbers like \(1.234\). They could even be irrational numbers like \( \sqrt{2} \) or transcendental numbers like π, e, or ϕ, numbers with an infinite number of digits.

But look at the above examples — they all use integers for \( a \) and \( b \). Why make things harder than they have to be?

Besides, where we're headed there is nothing but integers.

A Little More Math (Elementary School Level)

There are a few basic concepts of arithmetic that you should have learned in your first year or two of school. They can be dressed up with fancy names, but the concepts or rules are very simple.

Let's say that all we have is addition and negation. Here are the rules with formal names, and some with simpler explanations. I'm using a fancy script 𝒪 to represent zero, as you will see that in more advanced discussion of elliptic-curve cryptography.

Addition — adding zero does nothing: $$ P + 𝒪 = P $$ $$ 𝒪 + P = P $$

Inverse or Negation: $$ P + (-P ) = 𝒪 $$ That leads to the invention or discovery of subtraction: $$ P + ( -P ) = P - P = 𝒪 $$

Commutative — order doesn't matter: $$ P + Q = Q + P $$

Associative — grouping doesn't matter: $$ (P + Q) + R = P + (Q + R) $$

What you learned as a young child is true for integers. $$ 7 + 𝒪 = 7 $$ $$ 7 - 7 = 𝒪 $$ $$ 2 + 3 = 3 + 2 $$ $$ (2 + 3) + 4 = 2 + (3 + 4) $$ And:

Multiplication can be built from addition: $$ 2 \cdot P = P + P $$ $$ 3 \cdot P = P + P + P $$ $$ Q \cdot P = P + P + ... + P $$ The last one is \( Q \) copies of \( P \) added together.

The Same Rules Apply On Curves

We can say that if E is the set of points on some elliptic curve, then we can do arithmetic on those points. And, the above rules apply.

What we're about to see is that we do arithmetic on those curve points in a way that I did not expect. Each point has some (x,y) coordinates, and I expected arithmetic on those points to be like vector addition, or dot products, or cross products. Not at all! But the important thing is that the same rules and relationships apply.

Seeing This In Pictures

Let's select one curve out of the above collection, the one where \( a = -1 \) and \( b = 2 \). $$ y^2 = x^3 - x + 2 $$

Let's select two points on that curve, P and Q. Each would be defined in terms of x and y coordinates satisfying the curve's equation. $$ P = ( x_P, y_P ) $$ $$ Q = ( x_Q, y_Q ) $$ We don't want to bother with solving cubic equations here, it's enough to know that we could if we had to.

Good news — we won't have to!

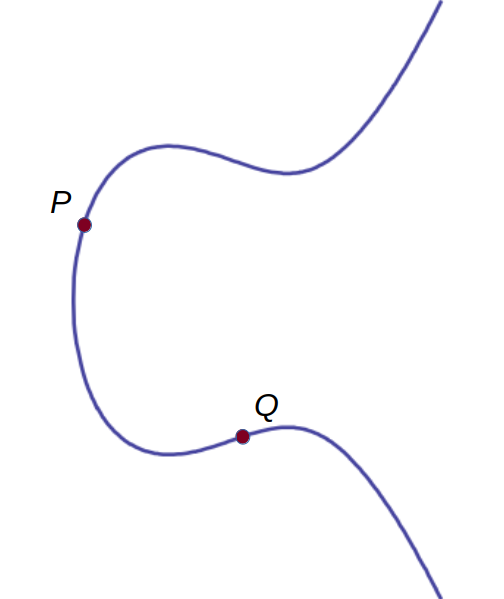
Here's where it starts to get a little weird.

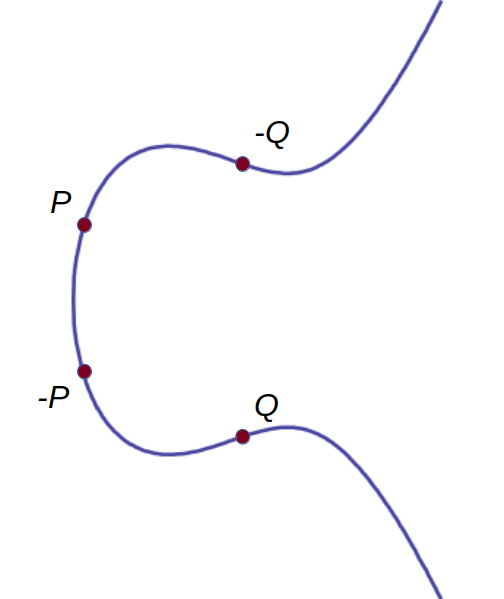
To negate a point, you replace its y coordinate with its negation. You reflect the point's position across the x axis. $$ P = ( x_P, y_P ) $$ $$ -P = ( x_P, -y_P ) $$ $$ Q = ( x_Q, y_Q ) $$ $$ -Q = ( x_Q, -y_Q ) $$

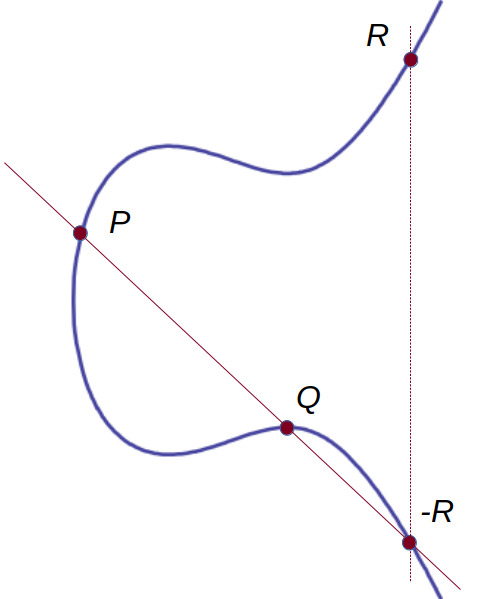
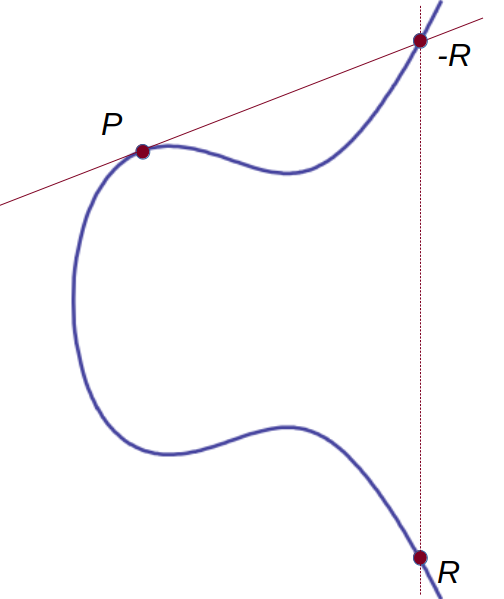
Most of the time, a line through two points on an elliptic curve also intersects the curve at a third point.

Most of the time. There are two exceptions. One is a vertical line, which continues up and down to infinity with no third intersection.

Notice: "to infinity with no third intersection."

The formal terminology is: "An elliptic curve is the set of points satisfying $$ y^2 = x^3 + ax + b $$ plus a point 𝒪 at infinity."

So, "point 𝒪" means there's no such point, even infinitely far up and down the vertical line. OK.

Here's where it gets more weird, or at least more unexpected, at least for me.

We want to do arithmetic using points on the curve. We want to calculate: $$ P + Q = R $$

We can do this graphically. Draw a line through \( P \) and \( Q \). As long as \( Q \neq -P \) the line will also intersect the curve at a third point. That third point is \( -R \).

Negate that point \( -R \) and there's your answer, \( R \).

So if we add \( P \) and \( -P \), meaning if we subtract, we get $$ P + ( -P ) = P - P = 𝒪 $$ That is, a vertical line with "intersection at infinity", actually no intersection at all, so zero.

One last piece we need is doubling, or multiplying by 2.

As \( P \) and \( Q \) come closer to each other, the point \( Q \) approaches becoming equal to \( P \). The line passing through \( P \) and \( Q \) approaches simply being the tangent to the curve at \( P \). When \( Q \) actually is \( P \), then the line is the tanget to the curve at \( P \) and it intersects the curve at \( -R \). Here's the other exception to the rule that every line through two points intersects the elliptic curve at a third point. We can graphically calculate: $$ P + P = 2 \cdot P = R $$

The Algebra — Feel Free To Skip

The good news is that the algebra for calculating the coordinates of the answer has already been worked out for us.

The even better news is that we won't need to get into those details! If you want, feel free to jump ahead to the last page.

Jump to:
Points on a Curve

But to be complete, here is how to calculate the coordinates. No need to draw lines and measure intersections. Just plug the coordinates of P and Q into some fairly simple equations.

If the curve is: $$ y^2 = x^3 + ax + b $$ then to calculate \( R \) in: $$ P + Q = R $$ where \( P \neq Q \) and: $$ P = ( x_P, y_P ) $$ $$ Q = ( x_Q, y_Q ) $$ $$ R = ( x_R, y_R ) $$ you do it this way: $$ \lambda = \frac{ y_Q - y_P }{ x_Q - x_P } $$ $$ x_R = \lambda^2 - x_P - x_Q $$ $$ y_R = \lambda( x_P - x_R ) - y_P $$

To calculate \( R \) in: $$ P + P = 2 \cdot P = R $$ you do it this way: $$ \lambda = \frac{ 3 {x_P}^2 + a }{ 2 y_P } $$ $$ x_R = \lambda^2 - 2 x_P $$ $$ y_R = \lambda( x_P - x_R ) - y_P $$

If, on the other hand, the curve is: $$ y^2 + xy = x^3 + ax^2 + b $$ then to calculate \( R \) in: $$ P + Q = R $$ where \( P \neq Q \), you do it this way: $$ \lambda = \frac{ y_Q + y_P }{x_Q + x_P} $$ $$ x_R = \lambda^2 + \lambda + x_P + x_Q + a $$ $$ y_R = \lambda( x_P + x_R ) + x_R + y_P $$

To calculate \( R \) in: $$ P + P = 2 \cdot P = R $$ you do it this way: $$ \lambda = x_P + \frac{ y_P }{ x_P } $$ $$ x_R = \lambda^2 + \lambda + a $$ $$ y_R = {x_P}^2 + \lambda x_R + x_R $$

That's it for the algebra formulas! On to the last page:

Points on a curve