Bob's Blog

What's the Point of Asymmetric Encryption?

As I complained earlier, cybersecurity certifications require students to memorize a lot of nonsense.

Some of it is ancient history, such as adding a new question topic about Thicknet cables around 2015, well over a decade after most organizations had abandoned that technology.

Some, however, is even worse — you are required to memorize utter nonsense. The "correct" choice to get the point for the question is actually wrong in the real world.

One of those exam fictions is about asymmetric encryption. That is an extremely important topic. We can't safely use the Internet without properly using asymmetric encryption. I have had to explain what you must select for the exams so many times that I can quote the fiction out of habit if I'm not careful!

Let's see what asymmetric encryption is really used for, why it's some important, and why we're worried about the threat posed by quantum computing.

Symmetric Versus Asymmetric

Symmetric means that something is the same on both sides, like a water glass that has no left versus right side, or front versus back. A coffee mug or tea cup, however, is asymmetric, it has a handle on one side but not on the other.

We already had those concepts and words and so we applied them to ciphers, algorithms used to encrypt and decrypt messages.

A symmetric cipher must use the same key for both encrypting and decrypting. The person sending the sensitive message, or storing the sensitive information, is free to choose an encryption key. But once they have encrypted the data with that key, anyone wanting to decrypt it must use precisely that same key.

This means that you need a shared secret key if you're sending a message to someone else. It's very difficult to share a secret safely. But until relatively recently, symmetric ciphers were all we had.

In the 1960s, mathematicians at GCHQ and the NSA developed asymmetric ciphers. Academic researchers independently discovered them and published descriptions starting in the mid to late 1970s. Asymmetric means something isn't the same on both sides, and an asymmetric cipher uses a key pair. You could use either key to encrypt the data. But then you must use the other key of the pair to decrypt.

You usually refer to your key pair as the private key and the public key, and you treat them as their names suggest. You want other people to know your public key, so they can securely communicate with you. But they mustn't know your private key, because that would let them decrypt your secret data, convincingly masquerade as you, and do other terrible things.

The two keys are mathematically related, but in such a way that an attacker can't use your public key to derive your private key.

Well, "can't" is too strong of a word. An attacker could, in theory, use your public key to figure out what your private key is. However, based on the mathematics of the specific cipher, and what we can estimate about the attacker's budget and motivation and patience, we can be confident that it would almost certainly take them so long to do so that we no longer care about that risk.

Asymmetric ciphers tend to be based on trapdoor functions, math problems that are much harder to do in one direction than the other.

See the next blog entry if you're interested in learning about how those mathematically tricky asymmetric ciphers actually work. For now it's more than enough to know that the two major categories, so far, are RSA and Elliptic Curve Cryptography or ECC. Both allow us to increase key lengths, greatly increasing the difficulty of discovering a private key.

The security of RSA is based on the difficulty of factoring the product of two large prime numbers. Really large prime numbers, each of them hundreds of digits long. The security of ECC is based on the difficulty of solving something known as the Discrete Logarithm problem. As with RSA, it's extremely difficult to find a solution, but it's relatively easy to check whether a proposed solution is correct.

Let's see what the certification exams get horribly wrong about asymmetric ciphers, and what you need to know in order to function in the real cybersecurity world.

Dangerous Slogans

According to the nonsense that the certification exams make you memorize while studying, and then regurgitate while doing the exam and selecting what they see as the "correct answer", there is a pair of slogans about a pair of terms regarding encryption. Given that certification exam questions tend to be in a "pick one of four choices" format, that "pair of pairs" form is especially attractive to people authoring exam content. Those slogans are:

Given their wild assumption that the above is close enough to true, they can create questions like the following:

Here we see the typical trick of creating multi-stage or multi-level questions, in which one question becomes several. The first stage is acronym memorization, requiring you to know what "RSA" and "3DES" refer to. The first is an asymmetric cipher, the second is a very outdated (described in the early 1980s, replaced in 1991) symmetric cipher.

The second stage is knowing that ciphers protect confidentiality, while hash functions don't protect integrity but they do detect modification. Since both RSA and 3DES are ciphers and not hash functions, we can eliminate C and D.

The third stage is memorizing their faulty pair of slogans. And so, the "correct answer" on the exam would be A, while that simply would not work in the real world! The more you know about cybersecurity, the worse you will do on these exams.

There's also their common trick of hiding the actual question within a lot of irrelevant text. This field isn't that difficult, so the exams include lots of tricks to make your score worse.

Let's break down how wrong that slogan pair is.

As for the first slogan, of course the symmetric ciphers that we use today are computationally efficient. Why would anyone choose an inefficient algorithms? Those algorithms should be efficient because our data sets grow and grow.

As for the second slogan, the actual truth is that asymmetric ciphers are utterly impractical for anything worthy of being called a "file".

The certification exam authors were so taken by the symmetric–asymmetric and large–small pair of pairs that they threw out the important information. The reason that we need asymmetric ciphers is in that throwaway phrase about doing things in addition to "encrypting small files".

And, certainly not "files" but instead "small pieces of data". Quite small, no larger than 64 bytes in today's situations.

A pair of slogans that is useful is:

Protect the data with symmetric encryption.

Protect the keys and authentication with asymmetric encryption.

Why Not a File?

When you look at how RSA and ECC really work, you find that they are designed to operate on numbers.

Integer math operations on 128-bit, 256-bit, and 512-bit numbers run quite fast on computers, despite the size of those numbers:

$ bc -l
2^128
340282366920938463463374607431768211456
2^256
115792089237316195423570985008687907853269984665640564039457584007913129639936
2^512
13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084096
^D

However, a megabyte is 8 million bits, and we want to easily handle multi-megabyte files. So, no, asymmetric ciphers are not intended to operate on files.

How Do We Really Use Asymmetric Ciphers?

Asymmetric ciphers become crucial components in cryptographic protocols — multi-step processes that use cryptographic functions for their individual steps. The asymmetric ciphers handle symmetric cipher keys up to 256 bits long, and hash function outputs up to 512 bits long, and that's it.

These protocols aren't the obvious things people first think of, but they are absolutely critical for accomplishing what we need.

One of these is key agreement, establishing that elusive but crucial shared secret key. It will be a key for a symmetric algorithm, as we use symmetric encryption to protect confidentiality. And it will be a session key, meaning that it will only be used for a limited time to protect a limited amount of data.

Another requirement is combined sender authentication and data integrity, something achieved by a digital signature which requires asymmetric encryption to create, and the corresponding asymmetric decryption to verify.

Key Agreement with Asymmetric Ciphers, for Email Messages and Files

Let's say that I want to send a message to you. I want confidentiality, so that only you can read it. And it won't just be the word "Hello!", it will be a large message. Maybe a multi-megabyte picture accompanied by a detailed description, or a PDF file that includes lots of text and several images.

Step 1: I would first generate a new, random, 256-bit value. That will be the session key.

Step 2: Next, I would use that session key to encrypt the message, using the AES symmetric cipher in what's known as CBC or cipher block chaining mode. That's a strong cipher, being used in a way appropriate for files of significant size, with a unique one-time-only session key.

Step 3: Now I need to use your public key to encrypt that session key. Maybe you have an RSA key pair, so I apply the RSA algorithm with your public key to that session key.

Yes, the result is a symmetric key that has been encrypted by an asymmetric cipher. I need to be very certain that what I have really is your public key. I'll show you how to solve that once we get this message sent.

Step 4: I send you a composite message saying:

Here is a message that I encrypted using AES-CBC-256, using a session key that I'm including here after I encrypted it with your RSA public key. Here's the encrypted session key, and after that, the encrypted message.

Then the encrypted session key and the encrypted message are appended to that.

Now, I described it that way to make it a story that's reasonably easy to understand. The way this actually works makes it appear much simpler for the user. I would use an email tool that has a cryptographic plugin for PGP or S/MIME. When I first set it up, or when the organization's IT staff set it up for me, it was told how get public keys associated with email addresses.

When I composed an email to you containing some text and that picture, the plugin found the public key associated with your email address. It did the technical work of generating the random session key, encrypting that using RSA and your public key, and then encrypting the text and image components of the message using AES and the session key. Then it encoded all that ciphertext as ASCII so it could be handled by the email system. And then it created a data structure with some metadata explaining "This is an S/MIME message, so here is the AES-CBC-256 session key encrypted with such-and-such public key, here is a text piece encrypted with that session key, here is an image encrypted with that session key, ..." and so on.

Your email tool then uses a similar plugin to read the metadata and figure out how to decrypt and present the message to you.

There's no requirement that we send everything around by email! Similar tools let us do the same thing for files, so the file starts with a header explaining here's the RSA-encrypted symmetric session key, and then here starts the encrypted data.

Making Sure I Have Your Public Key

I mentioned above that I must be absolutely certain that I have your public key. Anyone can generate a key pair and associate any email address and other identity information with it, and then try to trick me into using that to send them the sensitive information that only you should receive. We can require and prove ownership of public keys using asymmetric encryption, here's how:

We need to have our public key in the form of a digital certificate. That's a complicated data structure that contains:

• Information about the owner of the key pair. Email address, a person's name or an organization's name, maybe an address, whatever is relevant to the situation.
• The owner's public key.
• Metadata about what type of public key it is.
• And some metadata created by the issuer, including:
  • Information about the issuer.
  • Start and end dates of validity.
  • A serial number.
  • A URL where you could check to make sure that the issuer hasn't revoked it.

All of that is then wrapped within a digital signature created by the issuer. The terms are very similar, don't get confused:

• A digital certificate is a data structure, it's a public key wrapped with some information that lets us verify that we should believe that the public key belongs to a particular person or organization.
• A digital signature is the result of a cryptographic operation that provides "proof of content" and "proof of origin". That is, it lets you verify that a piece of data has not been modified at all, and that it came from exactly one person or organization. Phrasing this a different way, a digital signature provides both data integrity and sender authentication.

A digital signature is created by a certificate authority or CA. Everyone involved needs to be very confident that they have a copy of the CA's public key, and that they can safely trust whatever the CA says about identity and the ownership of public keys.

The certificate authority for your work email might be an office within your organization. Or, companies such as DigiCert provide this as a service.

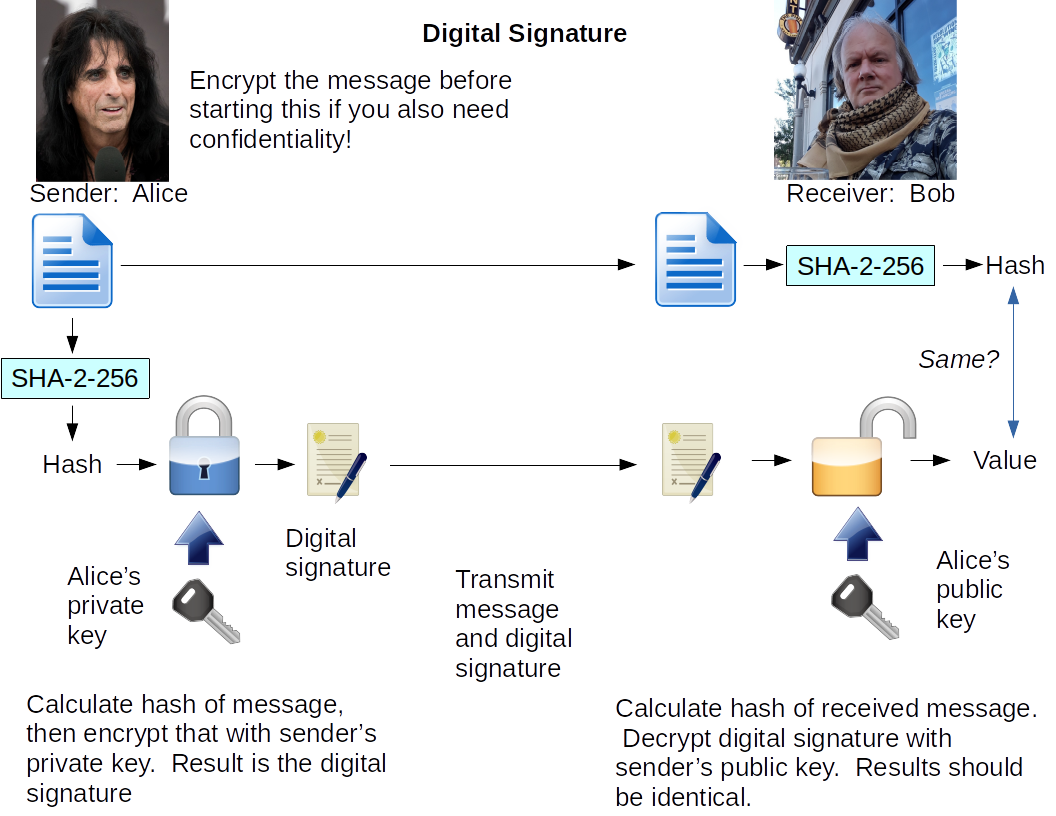
Now, how do you make a digital signature for a data structure such as one of these certificates?

1. Calculate the hash of the data.
2. Encrypt that hash using an asymmetric cipher with the issuer's private key.
3. Send the data and the digital signature to the receiver, with some metadata telling which hash function and which asymmetric cipher were used, and who created the signature.

And how do you verify a digital signature for received message?

1. Read the metadata to see which hash function and asymmetric cipher to use, and which CA public key to use.
2. Calculate the hash of the received message.
3. Decrypt the digital signature using the issuer's public key.
4. Verify that the output of steps 2 and 3 are identical. If the message was changed in transit by only one bit, the hash output will be radically different from what it should be. And if someone is trying to make fake signatures, they won't have the proper issuer's private key, so there's no way that decrypting with the actual public key will produce anything at all similar.

Pictures can make things much easier to understand, here's how it works:

Server Authentication and Key Agreement with Asymmetric Ciphers, for Web Connections

When your web browser connects to my server, the first thing that happened was that my server sent its digital certificate. In the case of my server, the certificate is from the Let's Encrypt organization.

Also, my server has two key pairs, both RSA and ECC, and so it would have sent two certificates. Your browser will prefer the ECC certificate because ECC is much faster than RSA. Unless, that is, your browser is so old that it doesn't support ECC.

Your browser knows the public keys for all the certificate authorities. That lets it verify that Let's Encrypt is saying "Yes, cromwell-intl.com exists, and the public key in this certificate really belongs to that server."

So, your browser is now convinced that it knows my server's public key. However, it doesn't yet have proof that that's who it has connected to. Anyone could make a copy of my server's certificate and send it out.

So, your server generates a random string of bits and issues a challenge: "If you're really cromwell-intl.com, then you have the corresponding private key. Encrypt this challenge string using that private key and send the result back to me."

When it receives the result, it decrypts that response using what it knows to be the server's public key. If the result is the same as the challenge it sent, then the response must have been encrypted with the server's private key, and so that must really be the server.

There will have been some back-and-forth in which the server and client exchange information about the suite of cryptographic functions that each one supports. They will have selected the best combination of what is supported at each end. Nowadays that probably includes AES in GCM or Galois Counter Mode, or the ChaCha20/Poly1305 stream cipher, for symmetric encryption.

The old way of proceeding is easier to explain, so I'll start with that. Your browser would make up a new 256-bit string, which will be the session key protecting the communication. It would encrypt that session key using the server's public key and send it over, saying "Please encrypt everything using AES and this session key, which was encrypted using your public key", and everything from there forward would be encrypted.

The modern way is called Elliptic-Curve Diffie-Hellman Ephemeral, which gets abbreviated as ECDHE because the name is quite a mouthful. It's based on the classic Diffie-Hellman logic, but using elliptic-curve crytography for speed, and agreeing up an ephemeral key. That provides something called perfect forward secrecy, which means that even if your adversary has been saving all your ciphertext in the hopes of someday breaking it, and then your private key is somehow exposed, that still doesn't let your adversary go back and decrypt any of those earlier messages or files.

How does ECDHE work? Well, this blog entry is already long enough! The short version for now is that both parties generate a new ECC key pair for each session. I have a page showing how ECDHE works, as part of a several-page story explaining elliptic curves and ECC in general. At some point I'll add a blog entry focused just on the ECDHE payoff.

Quantum Computing Sounds Interesting! Why is it Scary?

A general-purpose quantum computer could quickly solve the trapdoor problems on which RSA and ECC are built. While we know of no efficient solutions for factoring or discrete logarithms on a classic computer, we have known of efficient algorithms to solve them since the early 1990s.

Don't panic! Cryptographers have been developing replacements for which we don't know efficient solutions on any computer, classic or quantum. These new algorithms are call "quantum-resistent" or "quantum-safe" or "post-quantum".

Quantum-resistant cryptography is a topic for another blog entry!